This article is contributed. See the original author and article here.
What is Imbalanced Data?
For a given classification problem, if the classes/targets within the dataset are not represented equally, then the dataset is said to be imbalanced. The classes with a higher representation are called majority classes, while the ones with lower representation are called minority classes. Sometimes imbalance exists due to limited availability of data for certain classes, while in other cases it could be attributed to the nature of the dataset. For instance, if there is a spam classification dataset, we’d expect more non-spam emails than spam emails. Similarly, for fraud detection, we would expect the fraudulent transactions to occur only rarely.
It is harder for learning models to generate predictions for the minority classes because the model has access to limited training examples representing those classes, making it difficult for it to learn to distinguish these classes. Most ML algorithms for classification perform well when all classes have a roughly equal distribution and hence it becomes important to address the problem of class imbalance.
How do we detect class imbalance?
While there is no fixed definition of what constitutes an imbalance, generally it is detected using one of the following:
- Ratio of the samples in the least populated class to the overall number of samples in the dataset. Let’s call this Ratio-1.
- Ratio of the samples in the least populated class to the samples in the most populated class. Let’s call this Ratio-2.
Let’s evaluate both methods using a couple of sample cases:
- For a four–class problem with data distributed among labels like this: {‘a’: 20, ‘b’: 20, ‘c’: 20, ‘d’: 200}, Ratio-1 is 7.7%, while Ratio-2 is 10%.
- For a four–class problem with data distributed among labels like this: {‘a’: 20, ‘b’: 200, ‘c’: 200, ‘d’: 200}, Ratio-1 is 3.2%, while Ratio-2 is 10%.
As seen in the above examples, Ratio-2 remains consistent, even if the constitution of the other classes in the overall data changes.
Hence, we utilize Ratio-2 as the indicator of imbalance in AutoML and imbalance is detected when this ratio is lower than 20%.
How to address the problem of Imbalance?
Ideally one would prefer collecting more data for the minority class(es). However, often that is quite expensive or may not be feasible due to the nature of the problem (e.g., fraud or spam detection).
Therefore, we leverage the following methods for dealing with imbalanced data within AutoML:
- Using weights for class balancing: this feature gets automatically applied in AutoML if it improves performance on a subset of the user’s data (more details in later sections)
- Using metrics that are sensitive to imbalance: users can pick relevant metrics based on our recommendations.
- Leveraging the sample weights provided directly by the user via the AutoML config
Additionally, users can apply over/under sampling to rebalance the data before feeding it to AutoML. Methods #1 and #3 will impact the ML algorithm’s cost function in the same manner (covered in the next section), but the difference is that in method #1 AutoML will automatically do it for you. This feature of Class Balancing using weights is the focus of this blog and we shall elucidate that next.
Weights for Class Balancing:
Without actually over–sampling the minority classes or under-sampling the majority classes, we can simply apply weights to the samples belonging to a class, in the inverse proportion of the number of samples representing that class (Fig 1 elaborates on this calculation). The intent is that the underrepresented classes would have a higher weight than the overrepresented ones.
We leverage this method because it allows us to apply balancing without increasing the size of the dataset, and hence without modifying memory requirements. Additionally, even if the classes are well balanced, applying this method would simply apply uniform weights, and in theory this method could be applied for all datasets.
To understand the impact of applying weights, let’s review the cost function J(θ) for a Logistic Regression classifier below. Here m is the number of training samples, x and y are the features and labels respectively, θ refers to the model parameters.
When we use the Weights for Class Balancing, the above cost function is modified to apply the class weight corresponding to every training sample, as shown below, where c(i) refers to the class weight for the ith training sample.
Using metrics sensitive to imbalance:
For dealing with class imbalance we recommend using AUC–weighted as the optimization metric for AutoML runs. There are several benefits, as follows:
- Any macro average will independently calculate the average for every class and then take the overall average, thus treating all classes equally; whereas a weighted average will calculate the contribution of every class based on the relative number of samples representing that class, and hence this is more robust to imbalance. Hence, we choose a weighted metric.
- Additionally, AUC-weighted is threshold invariant since it measures the area under the (ROC) curve over all possible classification thresholds by aggregating them.
- We also report several other metrics sensitive to class imbalance, such as F1, Precision, Recall and Matthew’s Correlation Coefficient.
Analysis and Experimentation:
After selecting the solution and the metric, we performed A/B tests on a variety of datasets with the following setup:
- Treatment Group: using weights for treating class imbalance
- Control Group: with no class balancing
- Significance Level (Type 1 Error probability) preselected as 5%
- H0 (Null Hypothesis): There is no impact on the performance of AutoML after applying weight-balancing
- Ha (Alternative Hypothesis): Weight balancing improves the performance of AutoML
- One tailed t-tests were performed by leveraging the sample statistics like sample standard deviation from multiple runs performed on the same datasets
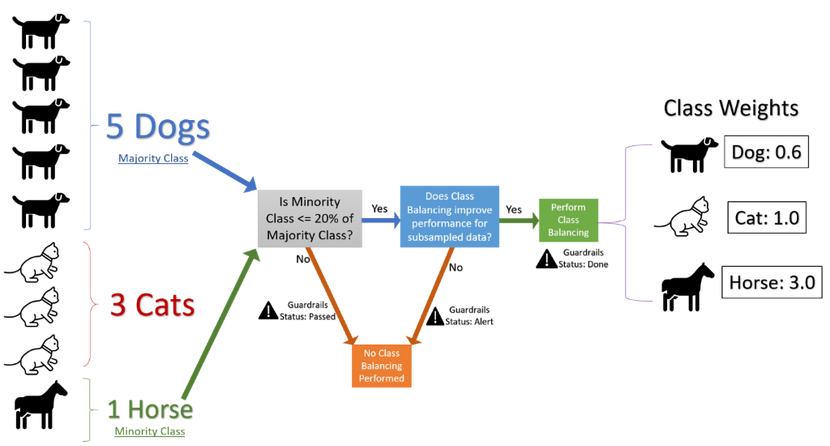
Extensive A/B testing with this setup demonstrated that we could leverage subsampled data reliably to determine the effectiveness of our class balancing solution. Running A/B tests on subsampled data rather than the full data enabled us to reduce the overall execution time. These tests utilize sample statistics computed using binomial distribution and some heuristics. This helps us decide if balancing the classes using weights would improve the performance and the complete flow is described in the graphic below.
Additionally, AutoML’s Guardrails feature informs the user if their data exhibits imbalance and if the class balancing solution was applied.
Figure 1: Flow chart describing the handling of imbalanced data within AutoML
If you’re getting started today with Microsoft Azure’s Automated Machine Learning, here are a couple of helpful links:
https://azure.microsoft.com/en-us/services/machine-learning/automatedml/
https://docs.microsoft.com/en-us/azure/machine-learning/concept-automated-ml#how-automated-ml-works
Contributors:
Arjun Singh – Data & Applied Scientist II
Anup Shirgaonkar – Principal Data & Applied Scientist
Brought to you by Dr. Ware, Microsoft Office 365 Silver Partner, Charleston SC.




Recent Comments